Workshop 7 - Dirichlet Multinomial

Sylvain SCHMITT

2020-10-06

Introduction

Setup

##          used (Mb) gc trigger (Mb) max used (Mb)
## Ncells 461322 24.7     997401 53.3   641322 34.3
## Vcells 885270  6.8    8388608 64.0  1753819 13.4

Some categorical observation

Distributions.

Distributions.

Mathematics

Dirichlet

Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet

Dirichlet - Distribution

Continuous multivariate probability ditribution

Multivariate generalization of beta the distribution

Conjugate of catgorical and multinomial distributions

Dirichlet - Definition

Parameters: categories \(K \geq 2\) and concentrations \(\alpha_1,...,\alpha_K|\alpha_i>0\)

Support: \(x_1,...,x_K|x\in(0,1),\sum_{i=1}^Kx_i=1\)

PDF: \(\frac{1}{B(\alpha)}\Pi_{i=1}^Kx_i^{\alpha_{i-1}}|B(\alpha)=\frac{\Pi_{i=1}^K\Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^K\alpha_i)}\)

Dirichlet - Example

The picture illustrates the case where \alpha_i = \alpha and we vary over time the parameter \alpha from 0.3 to 2.0.
The picture illustrates the case where \(\alpha_i = \alpha\) and we vary over time the parameter \(\alpha\) from 0.3 to 2.0.

Multinomial - Distribution

Parameters: number of trials \(n > 0\) and event probabilities \(p_1,...,p_K|\sum p_i=1\)

Support: \(x_i\in\{0,..,n\}|i\in\{1,..,k\},\sum x_i=n\)

PMF: \(\frac{n!}{x_1!...x_k!}p_1^{x_1}...p_k^{x_k}\)

Bernoulli: \(k=2,n=1\), Binomial: \(k=2,n>1\), Categorical: \(k>2,n=1\)

Multinomial - Example

Hardy-Weinberg principle: Multinomial(n,(\theta^2,2\theta(1-\theta),(1-\theta)^2))
Hardy-Weinberg principle: \(Multinomial(n,(\theta^2,2\theta(1-\theta),(1-\theta)^2))\)

Dirichlet multinomial

Parameters: number of trials \(n > 0\) and probabilities \(\alpha_1,...,\alpha_K>0\)

Support: \(x_i\in\{0,..,n\}|\sum x_i=n\)

PMF: \(\frac{(n!)\Gamma(\alpha_k)}{\Gamma(n+\sum\alpha_k)}\Pi_{k=1}^K\frac{\Gamma(x_k+\alpha_k)}{(x_k!)\Gamma(\alpha_k)}\)

\[LPMF(y|\alpha) = \Gamma(\sum \alpha) + \sum(\Gamma(\alpha + y)) \\- \Gamma(\sum \alpha+\sum y) - \sum\Gamma(\alpha)\]

Softmax - Normalized exponential function

Generalization of the logistic function to multiple dimensions.

\(\sigma:\mathbb{R}^K\to(0,1)^K\)

\(\sigma(z)_i=\frac{e^{z_i}}{\sum_{j=1}^Ke^{z_j}}\\i=1,...,K~and~z = (z_1,...,z_K)\in\mathbb{R}^K\)

Softmax - Example

## [1] 0.02364054 0.06426166 0.17468130 0.47483300 0.02364054 0.06426166 0.17468130

Single species distribution

Data

Models

Models summary.
Name Formula
\(B_0\) \(Presence \sim \mathcal{B}ernoulli(logit^{-1}(\alpha_0))\)
\(B_{\alpha}\) \(Presence \sim \mathcal{B}ernoulli(logit^{-1}(\alpha_0+\alpha*Environment))\)
\(B_{\alpha, \alpha_2}\) \(Presence \sim \mathcal{B}ernoulli(logit^{-1}(\alpha_0+\alpha*Environment+\alpha_2*Environment^2))\)
\(B_{\alpha, \beta}\) \(Presence \sim \mathcal{B}ernoulli(logit^{-1}(\alpha_0+\alpha*Environment+Environment^{\beta}))\)
\(B_{\alpha, \beta}2\) \(Presence \sim \mathcal{B}ernoulli(logit^{-1}(\alpha_0+\alpha*(Environment+Environment^{\beta})))\)
\(B_{\alpha, \beta}3\) \(Presence \sim \mathcal{B}ernoulli(logit^{-1}(\alpha_0+Environment^{\alpha}+Environment^{\beta}))\)

Stan code

data {
  int<lower=1> N ;                // # of individuals
  int<lower=1> K ;                // # of environmental descriptors
  int<lower=0, upper=1> Y[N] ;    // individuals presence or absence (0-1) 
  matrix[N,K] X ;                 // environmental descriptors
}
parameters {
  real alpha ;       // intercept
  vector[K] beta ;   // sigmoidal slope
  vector[K] gamma ;  // quadratic form
}
model {
  alpha ~ normal(0, 10^6) ; // priors
  beta ~ normal(0, 10^6) ;
  gamma ~ normal(0, 10^6) ;
  Y ~ bernoulli_logit(alpha + X * beta + X .* X * gamma) ;
}

Predictions

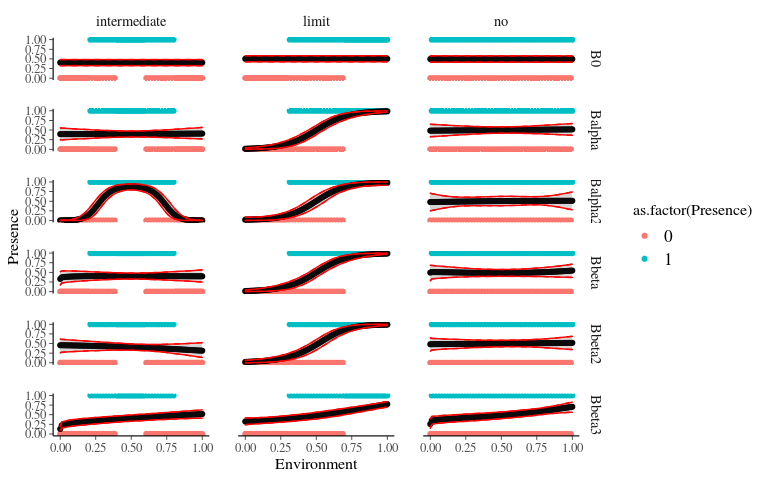
Predictions

Predictions.
Predictions.

Species joint distribution

Data

Model

\[Presence \sim \mathcal{Dirichlet~Multinomial}(\\softmax(\alpha + \beta*E + \gamma*E^2))\]

\[LPMF(y|\alpha) = \Gamma(\sum \alpha) + \sum(\Gamma(\alpha + y)) \\- \Gamma(\sum \alpha+\sum y) - \sum\Gamma(\alpha)\]

Stan code - data

\[Presence \sim \mathcal{Dirichlet~Multinomial}(softmax(\alpha + \beta*E + \gamma*E^2))\]

data {
  int<lower = 1> N  ;       // # of individuals
  int<lower = 1> S  ;       // # of species
  int<lower = 1> K  ;       // # of environmental descriptors
  int<lower = 0, upper=1> Y[N, S]  ; // individuals presence or absence for each species
  matrix[N,K] X ;           // environmental descriptors
}

Stan code - parameters

\[Presence \sim \mathcal{Dirichlet~Multinomial}(softmax(\alpha + \beta*E + \gamma*E^2))\]

parameters {
  vector[S] alpha ; // intercept
  matrix[S,K] beta ; // sigmoidal slope
  matrix[S,K] gamma ; // quadratic form
}

Stan code - model

\[Presence \sim \mathcal{Dirichlet~Multinomial}(softmax(\alpha + \beta*E + \gamma*E^2))\]

model {
  alpha ~ normal(0,1) ;  
  for(k in 1:K){
    beta[,k] ~ normal(0,1) ;
    gamma[,k] ~ normal(0,1) ;
  }
  for (n in 1:N)
    Y[n] ~ dirichlet_multinomial(softmax(alpha + 
                                         beta*to_vector(X[n,]) + 
                                         gamma*to_vector(X[n,] .* X[n,])))  ;
}

Stan code - LPMF

\[LPMF(y|\alpha) = \Gamma(\sum \alpha) + \sum(\Gamma(\alpha + y)) \\- \Gamma(\sum \alpha+\sum y) - \sum\Gamma(\alpha)\]

functions {
  real dirichlet_multinomial_lpmf(int[] y, vector alpha) {
    real alpha_plus = sum(alpha);
    return lgamma(alpha_plus) + sum(lgamma(alpha + to_vector(y)))
                - lgamma(alpha_plus+sum(y)) - sum(lgamma(alpha));
  }
}

Stan code - Full

functions {
  real dirichlet_multinomial_lpmf(int[] y, vector alpha) {
    real alpha_plus = sum(alpha);
    return lgamma(alpha_plus) + sum(lgamma(alpha + to_vector(y)))
                - lgamma(alpha_plus+sum(y)) - sum(lgamma(alpha));
  }
}
data {
  int<lower = 1> N  ;       // # of individuals
  int<lower = 1> S  ;       // # of species
  int<lower = 1> K  ;       // # of environmental descriptors
  int<lower = 0, upper=1> Y[N, S]  ; // individuals presence or absence for each species
  matrix[N,K] X ;           // environmental descriptors
}
parameters {
  vector[S] alpha ; // intercept
  matrix[S,K] beta ; // sigmoidal slope
  matrix[S,K] gamma ; // quadratic form
}
model {
  alpha ~ normal(0,1) ;  
  for(k in 1:K){
    beta[,k] ~ normal(0,1) ;
    gamma[,k] ~ normal(0,1) ;
  }
  for (n in 1:N)
    Y[n] ~ dirichlet_multinomial(softmax(alpha + 
                                         beta*to_vector(X[n,]) + 
                                         gamma*to_vector(X[n,] .* X[n,])))  ;
}

Fit

Trace

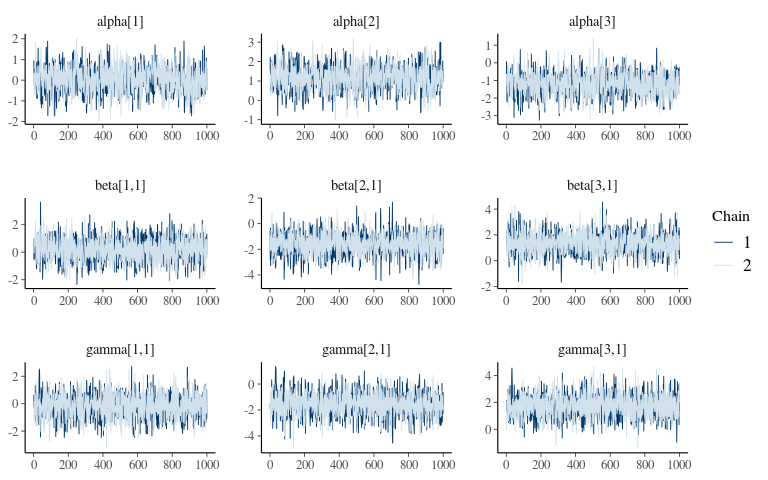
Trace plot.
Trace plot.

Pairs

Pairs plot.
Pairs plot.

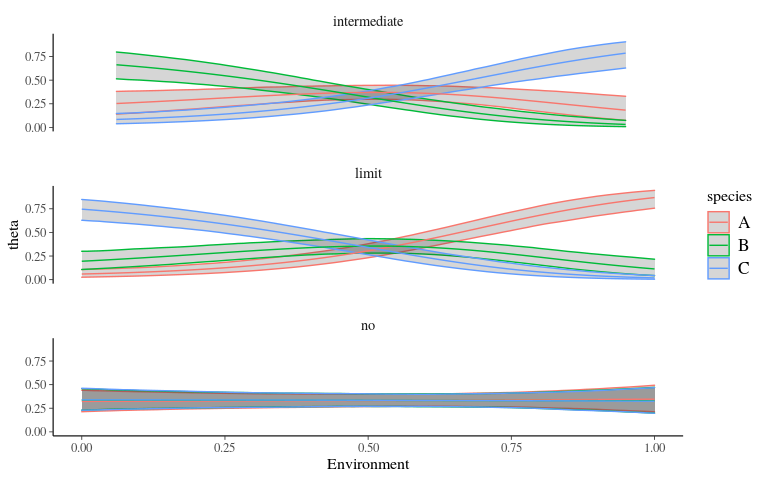
Predictions

Predictions

Predictions.
Predictions.

Species complexes in Paracou

Topographic Wetness Index

Topographic Wetness Index.

Topographic Wetness Index.

Neighbor Crowding Index

\[NCI_i = \sum _{j|\delta_{i,j}<20m} ^{J_i} DBH_j ^2 e^{-\frac{1}{4}\delta_{i,j}}\]

Posteriors

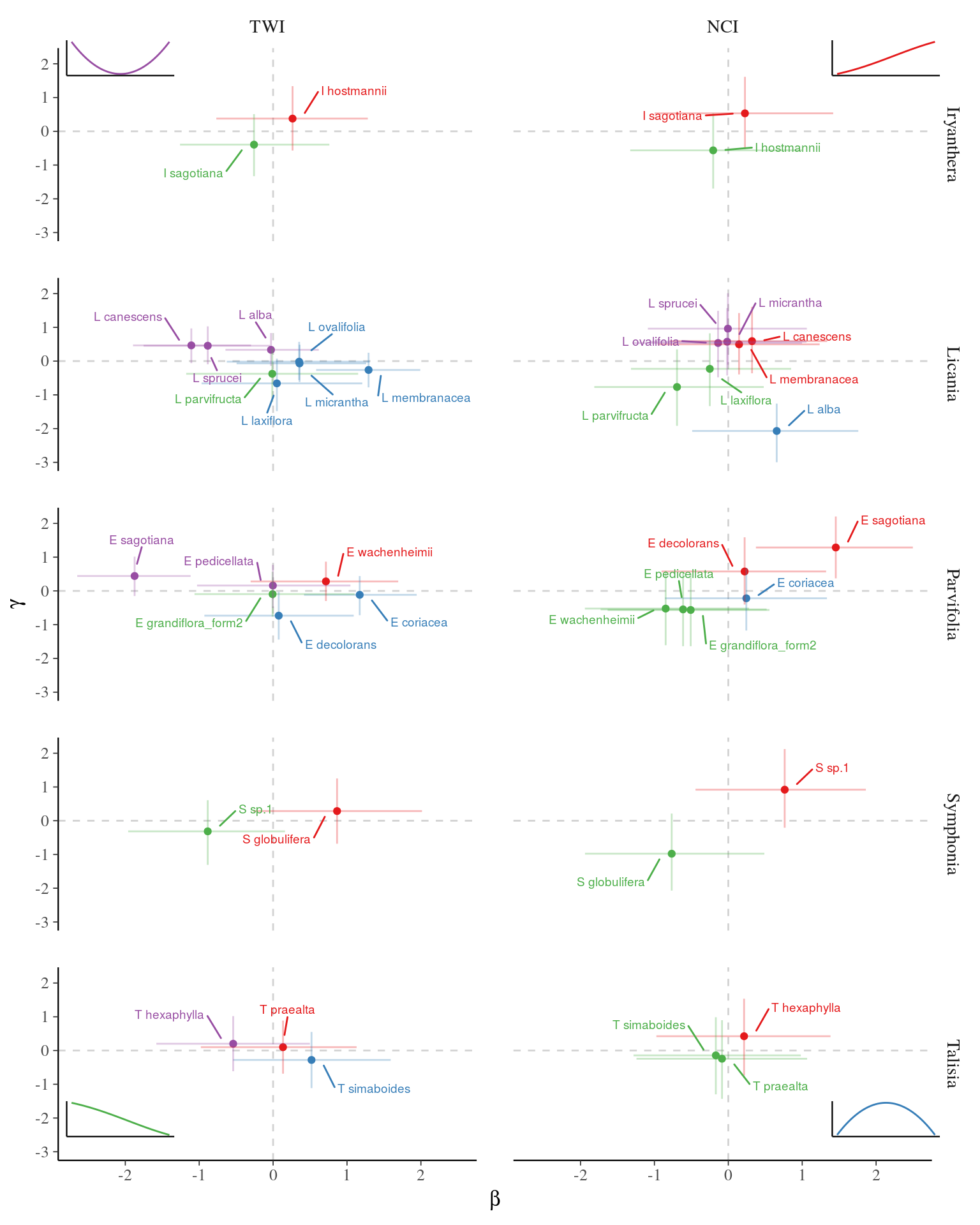
Posteriors.

Posteriors.

Predictions

Predictions.

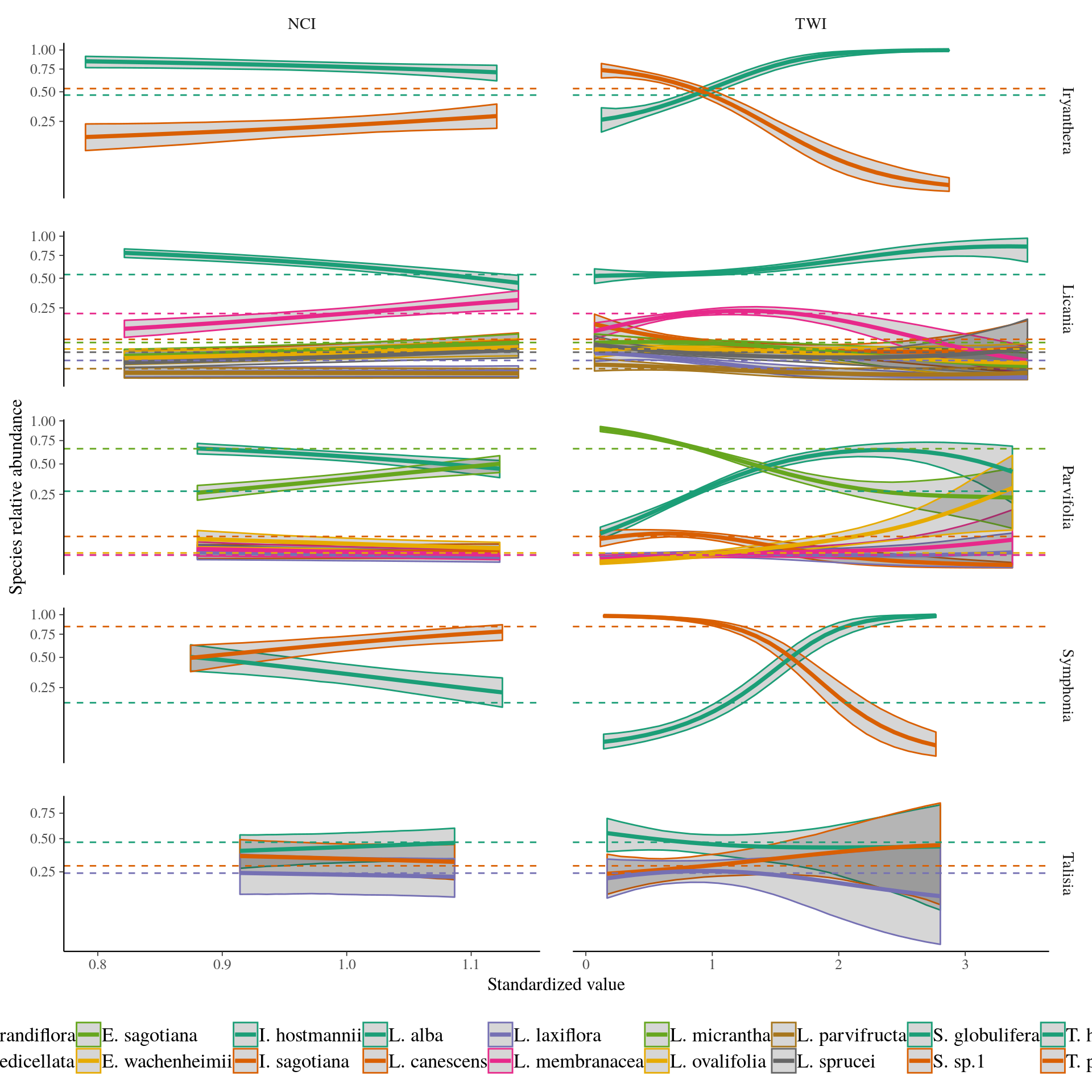
Predictions.